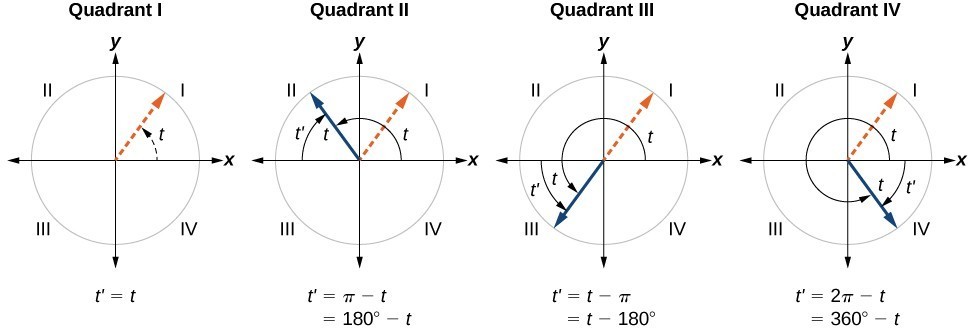
Since $\cos^2t\sin^2t=1$, dividing both sides by $\cos^2 t$ we also have $$1\tan^2t=\frac 1{\cos^2t}$$ Also, in the second quadrant, $\cos t0$ Use the second equation and the restriction to find $\cos t$, then use the first equation and the restriction to find $\sin t$ Then add those for your final answer(III) sin(π 6) = 1 2 cos(2 3 π) =cos(1 3 π) =1 2 tan(π 4) Prove tan(θ / 2) = sin θ / (1 cos θ) for θ in quadrant 1

Determine The Quadrant When The Terminal Side Of The Angle Lies According To The Following Conditions Sin T 0 Tan T 0 Study Com
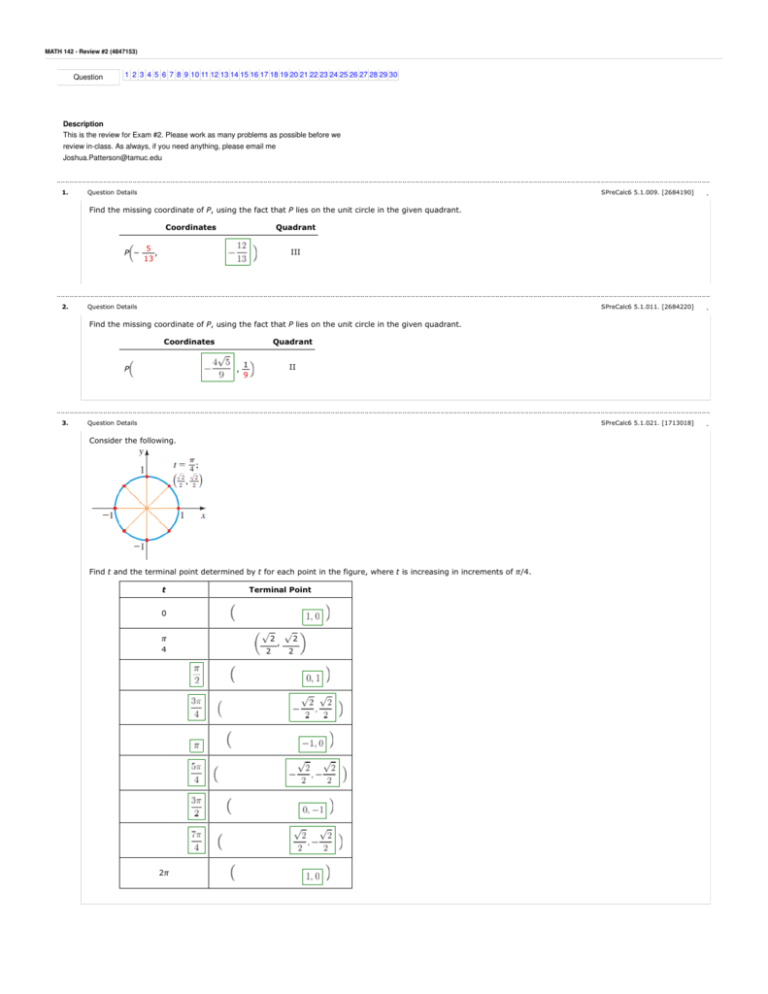
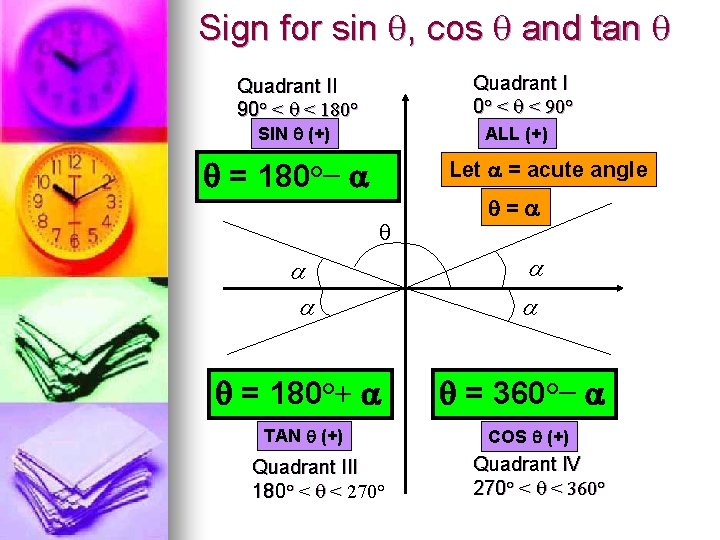
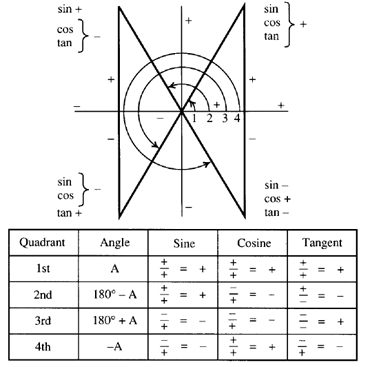
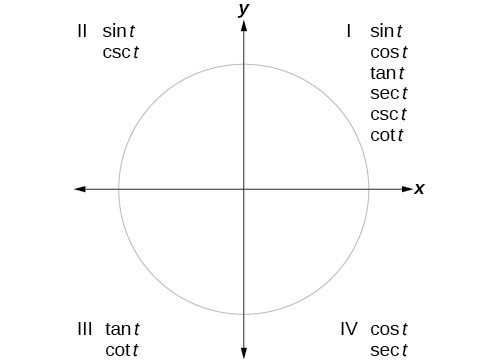
Quadrant 1 2 3 4 sin cos tan
Quadrant 1 2 3 4 sin cos tan- cos2x = (1tan^2x)/ (1tan^2x) = (1 (1/2)^2)/ (1 (1/2)^2) = (1 (1/4))/ (1 (1/4)) = (3/4)/ (5/4) = 3/5 tan 2x = sin 2x/cos2x = (4/5)/ (3/5) =4/3 answered by lilly Expert Please log in or register to add a comment if sinx=7/5 and angle x is in quadrant 2 and cos y=12/13 and angle y is in quadrant 1 find sin (xy) asked in TRIGONOMETRY by harvy0496 Apprentice doubleangle



1
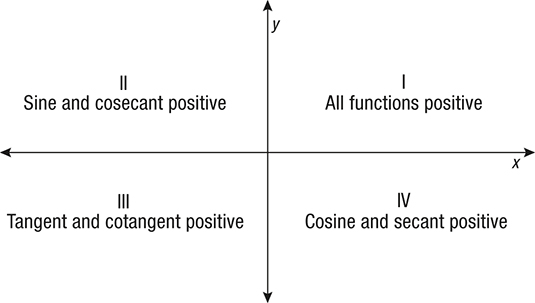
1 Answer Dean R tanθ = 3 4 means an opposite of 3, an adjacent of 4, so a hypotenuse of 5, because 32 42 = 52 cosθ = adjacent hypotenuse = ± 4 5 Sine and cosecant are positive in Quadrant 2, tangent and cotangent are positive in Quadrant 3, and cosine and secant are positive in Quadrant 4 Accordingly, why is sin positive in second quadrant?Click here👆to get an answer to your question ️ tanx = 4/3 , x in quadrant II Find the value of sinx/2, cosx/2, tanx/2
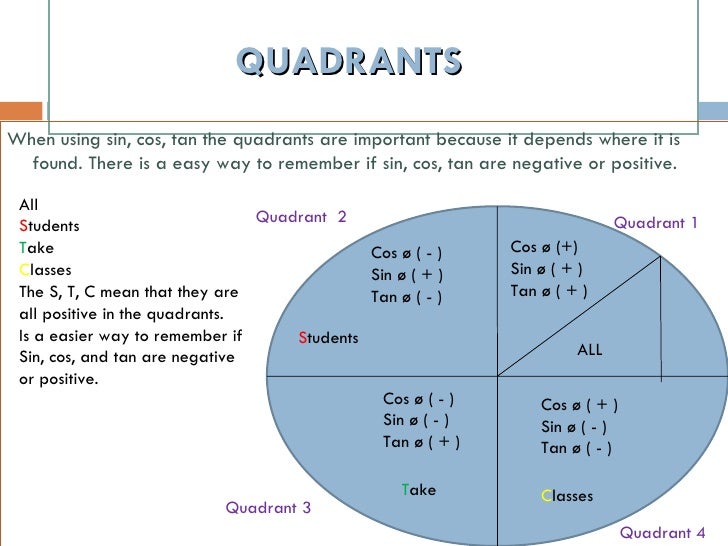
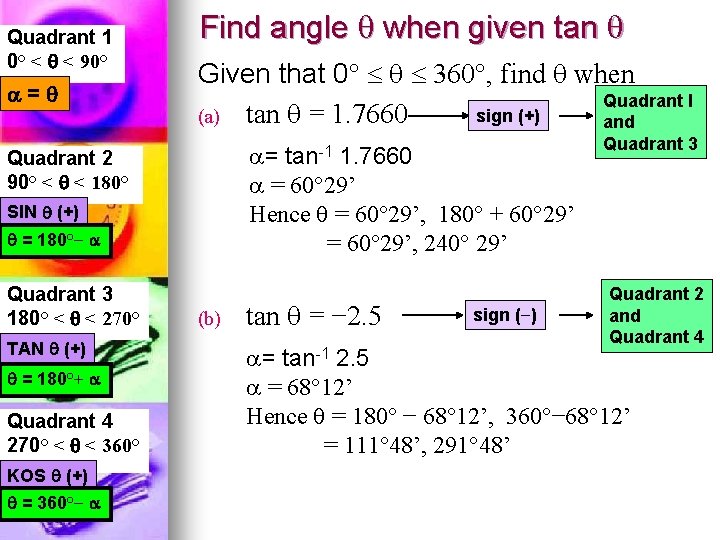
Quadrant 1 0° < < 90° = Find angle when given tan Given that 0° 360°, find when Quadrant I sign () (a) tan = 1 7660 and a= 1 7660 a = 60° 29' Hence = 60° 29', 180° 60° 29' = 60° 29', 240° 29' tan1 Quadrant 2 90° < < 180° SIN () = 180°− Quadrant 3 180° < < 270° TAN () = 180° Quadrant 4 270° < < 360° KOS () = 360°− (b) tan = − 2 5 sign (−) Quadrant 3 Quadrant 2Math tan (uv) given sin u=3/4 and cos v= 5/13 with U and V in quadrant 2 Use the identity tan (uv) = (tanu tanv)/1tanu tanv) Get the values of tanu and tanv from the sines and cosines that you are givenCos(θ) = − 1/3 θ in Quadrant III, sin(ϕ) = 1/4 ϕ in Quadrant II evaluate the expression math If sinθ=7/13 and cosθ=12/13 find tan θ and cot θ Use Pythagorean Identities to find sin θ and tan θ if cos θ =24/25 if the terminal side of θ lies in the third quadrant
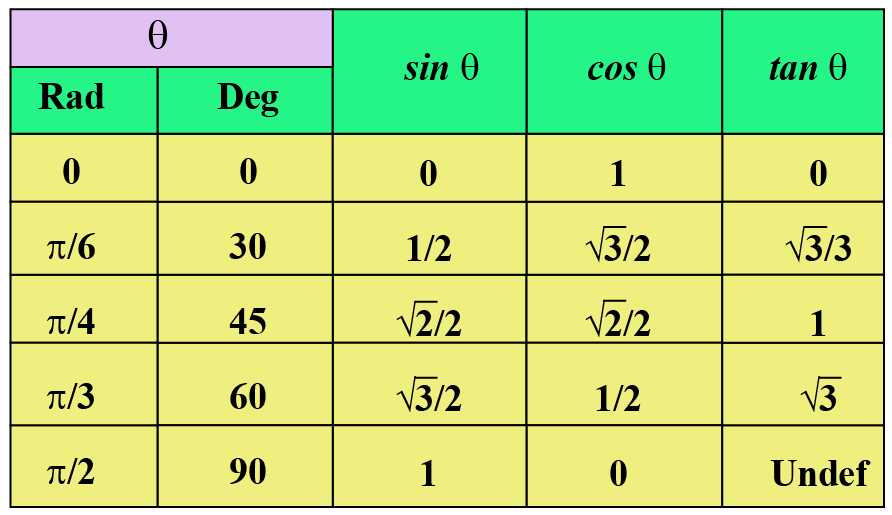
The angle of 225 degrees lies in the third quadrant and its value is 225–180 = 45 degrees below the xaxis Sine 45 in the third quadrant = (1/2^05) Cosine 45 in the third quadrant = (1/2^05)⇒ cos A = cos 2 4 0 0 ⇒ A = 2 4 0 0 Now, c o s B = − 2 1 ⇒ c o s B = − cos 6 0 0 when B does not lie in the third quadrant ⇒ c o s B = cos (1 8 0 0 − 6 0 0) ⇒ c o s B = cos 1 2 0 0 ⇒ B = 1 2 0 0 Substituting the value of A and B in equation (1) and we get, tan 1 2 0 0 sin 2 4 0 0 4 sin 1 2 0 0 − 3 tan 2 4 0 0 ⇒ tan (1 converting cos to sin and tan in specific quadrants Ask Question Asked 6 years, 1 month ago Active 6 years, 1 month ago Viewed 28k times 2 2 $\begingroup$ I'm having issues understanding as to how to go about doing this This is a table that expresses sin, cos and tan in terms of each other



完了しました Quadrant 1 2 3 4 Sin Cos Tan Quadrant 1 2 3 4 Sin Cos Tan Gambarsaeawp




List Of Trigonometric Identities Wikipedia
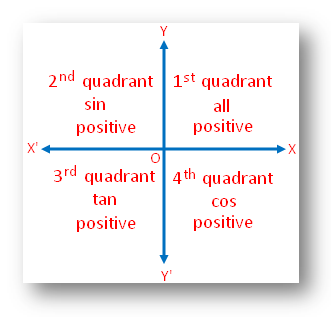
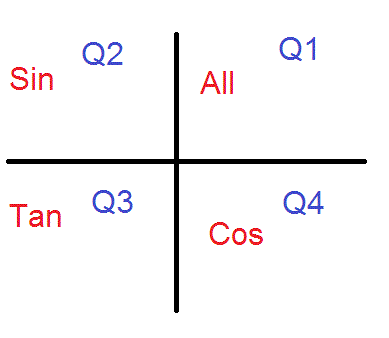
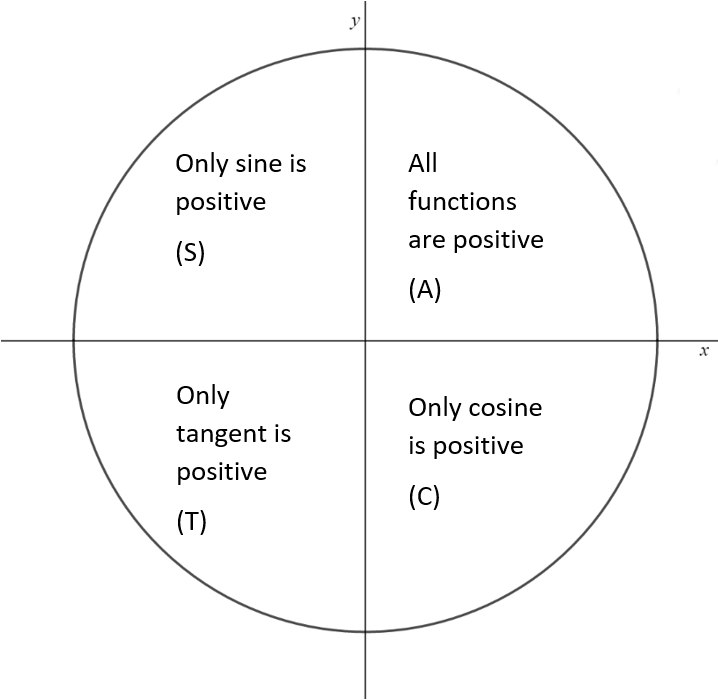
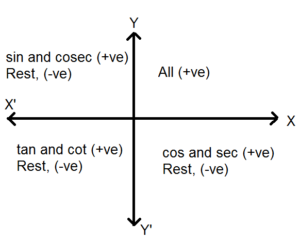
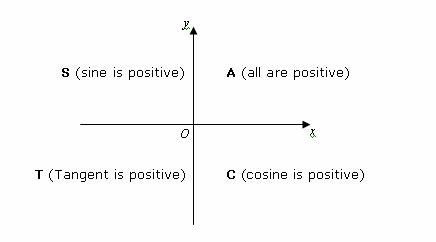
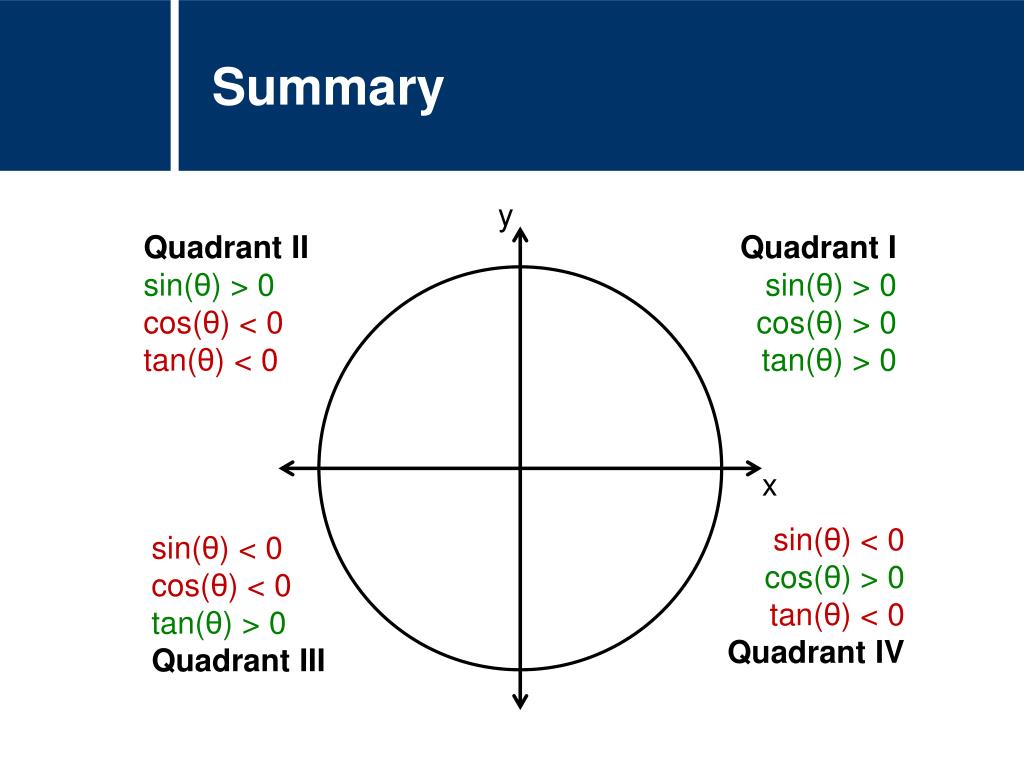
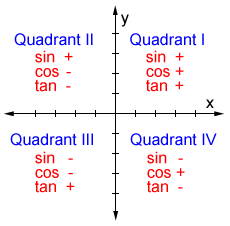
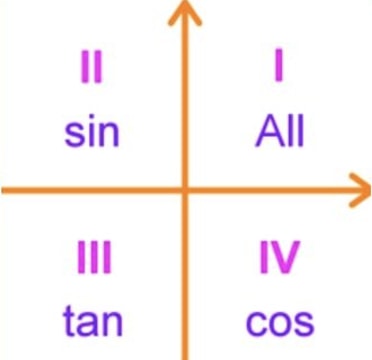
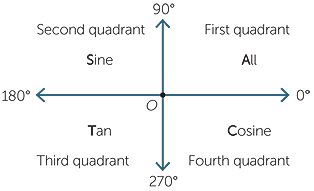
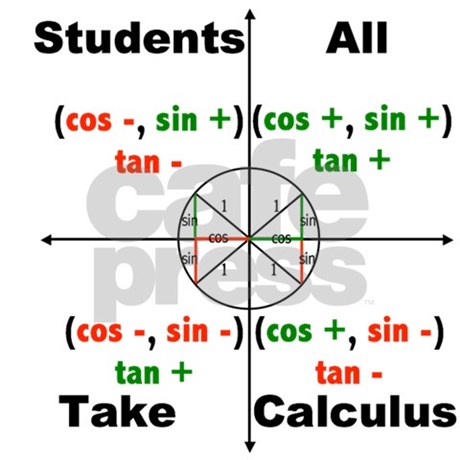
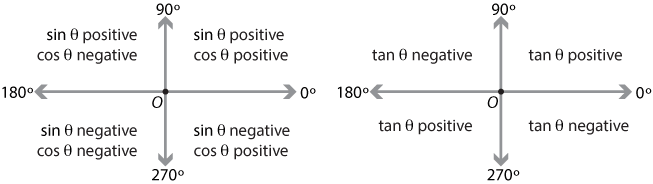
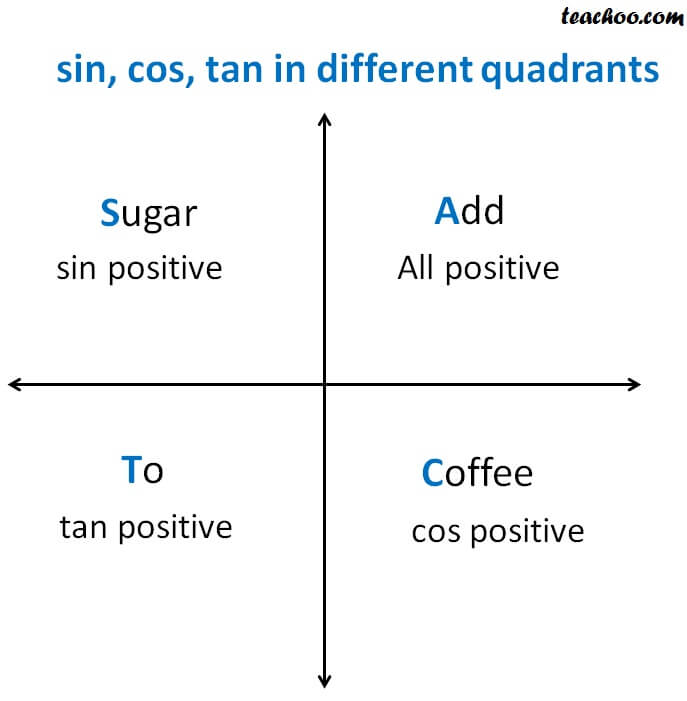
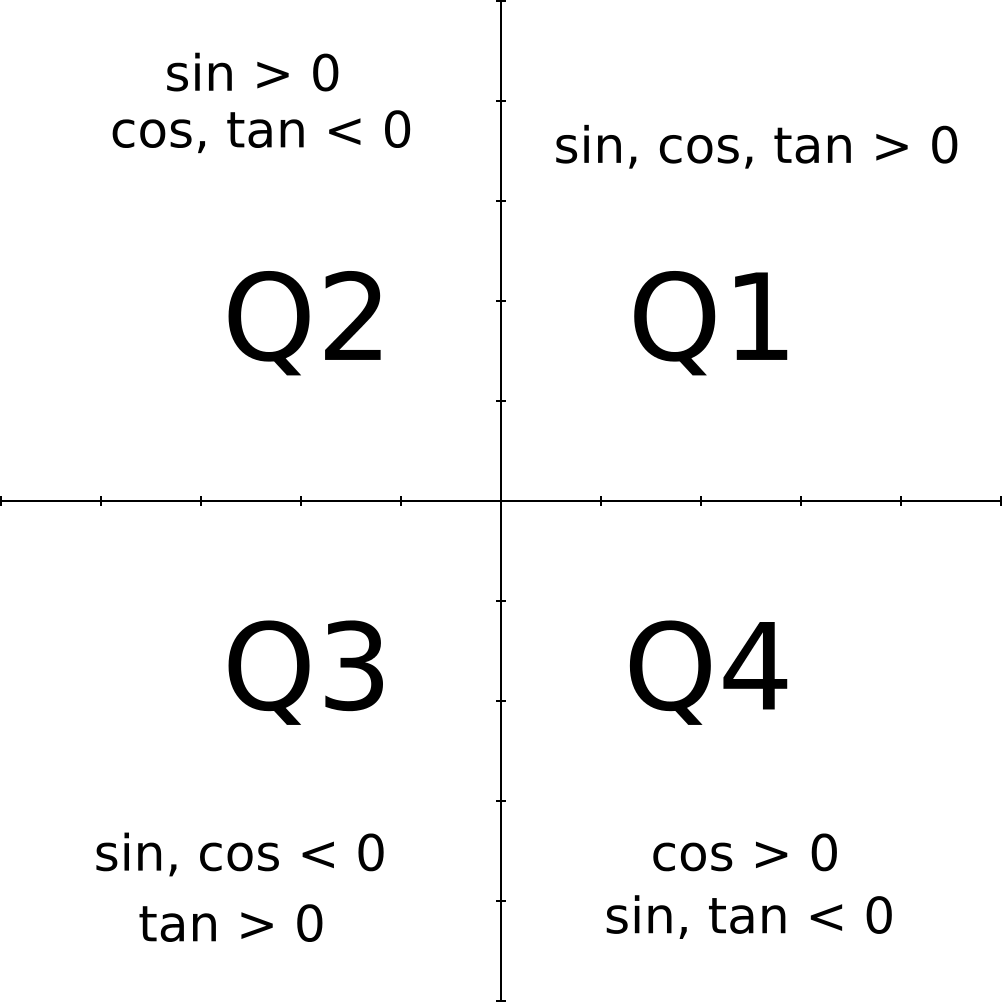
If tan x = 3÷4 wherex lies in third quadrant then find sin (x/2 ) , cos ( x/2) and tan (x/2) Get the answers you need, now!Frequently students ask why can't I work a double angle problem in the following way Suppose I am given sin(x) = 02, x is in Quadrant 1, and I am asked to find sin(2x)With a calculator, I can find the angle x (it's approximately o), double it (to get o), and then take the sine of that angle ()There is nothing wrong with this in practiceIn the second quadrant, the values for sin are positive only In the third quadrant, the values for tan are positive only In the fourth quadrant, the values for cos are positive only This can be summed up as follows In the fourth quadrant, Cos is positive, in the first, All are positive, in the second, Sin is positive and in the third quadrant, Tan is positive This is easy to remember, since



Trigonometry 1



1
Mathematics, 0700, harvzoie Sin x= 3/4 x in quadrant 1, find Sin(2x),cos(2x), tan (2x)Stanbon (757) You can put this solution on YOUR website! We know that sin^2 a cos^2 a= 1 ==> cos^2 a = 1 sin^2 a ==> cos^2 a = 1 (2/3)^2 ==> cos^2 a = 1 4/9 ==> cos^2 a= 5/9 ==> cos a = sqrt5/3 But a is in the 2nd quadrant where cos a ia



完了しました Quadrant 1 2 3 4 Sin Cos Tan Quadrant 1 2 3 4 Sin Cos Tan Gambarsaeawp



Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab
Find `Sin X/2, Cos X/2 and Tan X/2` of the Following `Sin X = 1/4`, X in Quadrant II CBSE CBSE (Arts) Class 11 Textbook Solutions 85 Important Solutions 12 Question Bank Solutions 7358 Concept Notes & Videos 503 Syllabus Advertisement Remove all ads Find `Sin X/2, Cos X/2 and Tan X/2` of the Following `Sin X = 1/4`, X in Quadrant IICoordinates Quadrant P , II 1 9 3 Question Details SPreCalc6 for the values of t whose terminal points are shown on the unit circle in the figure t increases in increments of π/4 t sin t cos t 0 π 4 π 2 3 θ in Quadrant III sin θ= tanLearn termquadrants = 1 2 3 4 with free interactive flashcards Choose from 500 different sets of termquadrants = 1 2 3 4 flashcards on Quizlet




Signs Of Trigonometric Ratios In Diffrent Quadrants Formed Due To Axes



6 Trigonometric Functions Of Any Angle
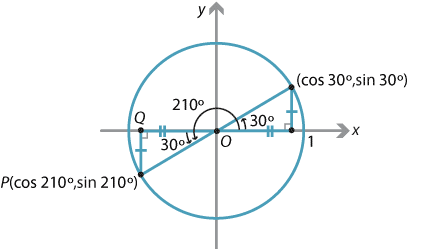
Course Title CHEMISTRY 4BM50;Cosine cos (210°) = −1732 / 2 = −0866 Tangent tan (210°) = −1 / −1732 = 0577 Note Tangent is positive because dividing a negative by a negative gives a positive In Quadrant IV, sine and tangent are negativeA) quadrant 2 or 3 b) Quadrant 2 sin , cos , tan Quadrant 3 sin , cos , tan c) 115°, 245° 13 14 Answers may vary For example, given P (x, y) on the terminal arm of angle , sin , cos , and tan 15 a) 25°, 155°, 5°, 335° b) 148°, 352 o c) 16°, 106 o, 196 o, 286 o 16 a) could lie in quadrant 3 or 4 5 233° or 307° b) could lie



All Sin Tan Cos Rule Signs Of Trigonometrical Ratios Trigonometric Ratios



If Sin Theta 0 And Tan Theta 0 Then In What Quadrant Is The Angle Theta Socratic
Solution Since x lies in quadrant III, π < x < 3π/2 Therefore, π/2 < x/2 < 3π/4 Hence, cos x/2, and tan x/2 are negative while sin x/2 is positive as x/2 lies in quadrant II It is given that cos x = 1/3 cos 2(x/2) = 1/3 By double angle formulas, 2cos 2 (x/2) 1 = 1/3 2cos 2 x/2 = 1 1/3 cos 2 x/2 = (2/3) × (1/2) cos 2 x/2 = 1/3 cos x/2 = ± √(1/3)X 3 cos x 3= 0 x = 0, $ 5 Ox x = 3^4 * X x = 6,7 ग 6'6Trigonometry Find the Other Trig Values in Quadrant I cos (s)=3/4 cos (s) = 3 4 cos ( s) = 3 4 Use the definition of cosine to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the values cos(s) = adjacent hypotenuse cos (




Trigonometry Quadrants And Quadrantal Angles




5 3 Trigonometric Ratios For Angles Greater Than 90o Ppt Download
You can put this solution on YOUR website!For an angle in the second quadrant the point P has negative x coordinate and positive y coordinate The angles which lie between 0° and 90° are said to lie in the first quadrant In the first quadrant, the values for sin, cos and tan are positive In the second quadrant, the values for sin are positive only In the third quadrant, the values for tan are positive only
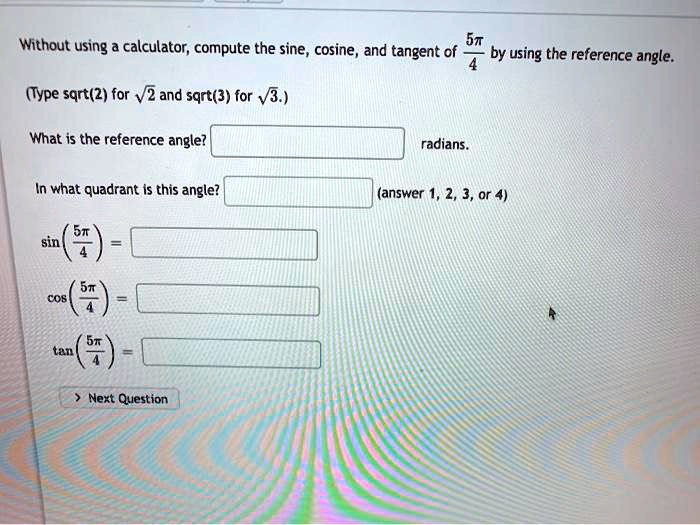



Solved Without Using Calculator Compute The Sine Cosine And Tangent Of St By Using The Reference Angle Type Sqrt 2 For 2 And Sqrt J For V3 What Is The Reference Angle Radians




Determine The Quadrant When The Terminal Side Of The Angle Lies According To The Following Conditions Sin T 0 Tan T 0 Study Com
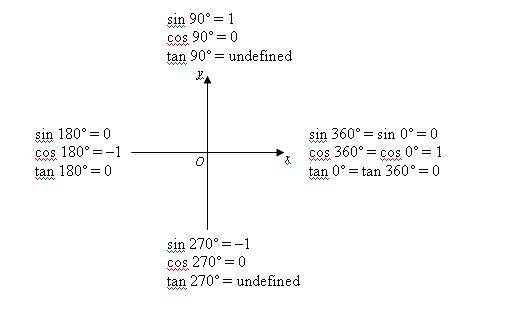
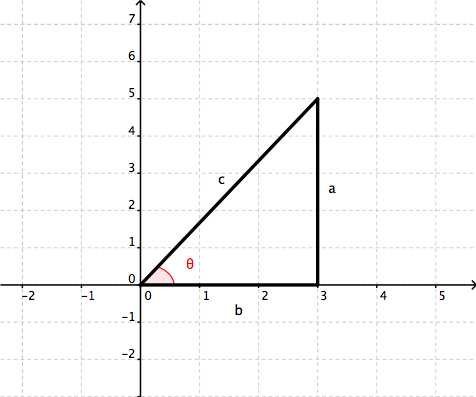
1answer Find the value of cos 2A, A lies in the first quadrant, when (i) cos A = 15/17 (ii) sin A = 4/5 (iii) tan A = 16/63 askedin Trigonometryby Anjali01(476kpoints) trigonometry class11 0votes 1answer The angle A lies in the third quadrant and it satisfies the equation 4 (sin^2x cos x) = 1 How do you evaluate the sine, cosine and tangent of 225 degrees without a calculator?10 r ( x, y) θ O y x Definition 21 Trigonometric Functions of a General Angle Let θ be an angle in standard position and suppose that ( x , y ) is any point other than ( 0 , 0 ) on the terminal side of θ(Figure 23)If r = x2 y2 is the distance between ( x, y ) and ( 0 , 0 ), then the six trigonometric functions of θ are defined by Using similar triangles, you can see that the values




04 Fundamental Trig
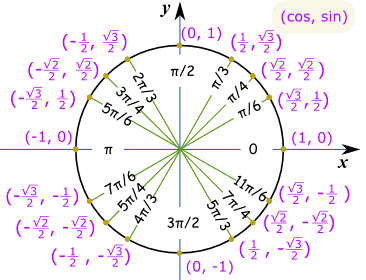



Easy Way Of Memorizing Values Of Sine Cosine And Tangent Mathematics Stack Exchange
Find an answer to your question Given, tanx = 4/3 Lies in 2nd quadrant Find sinx/2, cosx/2 and tanx/2Brainly User Brainly UserFor example, since sin(0)= 0 sin




Sine Cosine And Tangent In Four Quadrants



Find Sin X 2 Cos X 2 And Tan X 2 If Tan X 4 3 X In Quadrant Ii Sarthaks Econnect Largest Online Education Community
Answer to Find sin 2x, cos 2x, and tan 2x if cos x = 4 / 5 and x terminates in quadrant II By signing up, you'll get thousands of stepbystepTrigonometry Find the Other Trig Values in Quadrant I cos (theta)=8/17 cos (θ) = 8 17 cos ( θ) = 8 17 Use the definition of cosine to find the known sides of the unit circle right triangle The quadrant determines the sign on each of the values cos(θ) = adjacent hypotenuse cos ( θ) = adjacent hypotenuse Find the opposite side of theIf cos 0 = 3/4 and 0 in the 4th quadrant, find the exact value of the 5 other trig values opposite side of reference right triangle in quadrant IV =√(4^23^2)=√(169)=√7



Circular Functions Vce Methods




Trigonometry Section 5 1 In 1 4 Find 1 In Quadrant Ii 2 3 4 Use
Unending BE episode The third reel landed on a simple phrase 'Reroll x2' and while it was locked in place the other two reels spun again Tsunade was giddy about watching the machine spin No, she wasn't Tsunade was not giddy, a woman as refined and elegant as she was did not become giddy Tsunade reminded herself of this as sheWhen angle a is in Quadrant 3 (between 180° and 270°), both the adjacent and the opposite side are negative Hence, Sine and Cosine are negative and since Tangent (T) is a division between two negative numbers, it is the only trigonometric function that isIf A lies in the second quadrant and 3 tan A 4 = 0, then the value of 2 cotA – 5 cos A sin A is equal to `23/10` Explanation Given that 3 tan A 4 = 0



Section 4 4 Reference Angles Precalculus



Trigonometric Ratios Solutions Examples Videos
If A lies in second quadrant and 3 tan A 4 = 0, then the value of 2 cot A− 5 cos A sin A is equal to A −53/10 B 23/10 C 37/10 D 7/10 asked JunTherefore In Quadrant II, cos(θ) 0, sin(θ) > 0 and tan(θ) 0 (Sine positive) For an angle in the third quadrant the point P has negative x and y coordinates Therefore In Quadrant III, cos(θ) 0, sin(θ) 0 and tan(θ) > 0 (Tangent positive) For an angle in the fourth quadrant the point P has positive x coordinate and negative y coordinateTan a=4/3, condition pi/2 Cos b = 1/2, condition 0 Need exact value cos (ab) Sin (ab) Tan (ab) I believe a would be in quadrant 2 where x is negative and y is positive And b would bi



Signs Of Trigonometric Ratios In Diffrent Quadrants Formed Due To Axes




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2
Transcribed image text D Question 4 4 pts Given tan(x) = 1 and x in the IV quadrant sx's 2x), find the exact values of sin(), cos(?) and tan() sin($) T cos() = 4 tan = 1 3VI7 17 417 17 O sin() = S 34 cos() = tan($) = sin() = cos($) = 5 tan() Question 5 4 pts Find the solutions in 0,271) of the following equation 2 sin?Sin = 3 Quadrant IVcot = 6 cos = 4 Quadrant Icot = 8 sec = 5 Quadrant IIItan = 5 csc = 6 Quadrant IIcot = 3 sin = 7 Quadrant IIIcot = 2 tan = 8 Quadrant IItan = 2 cot = 9 Quadrant IIItan = 2 sec = 10 Quadrant IVcot = 3 sec = Quadrant Icot = 3 sin = 24 Quadrant IItan = 6 cos = Author Administrator Created DateSo cos(x/2) = 1/root(3), sin(x/2) = root(2/3), tan(x/2) = sin(x/2)/cos(x/2) = 2 2 tan(x) = 3/4 in 3rd quadrant, x lies in the 3rd quadrant and x/2 lies in the 2nd quadrant as seen in 1 tan(x) = 2tan(x/2)/1tan^2(x/2), 3/4 3t^2/4 = 2t (assuming tan(x/2) = t), 3t^2 8t 3 = 0, Discriminant = 8^2 4(3)(3) = 100,




If Sintheta 4 5 And Theta Lies In Third Quadrant Then The Value Of Cos Theta 2 Is Youtube
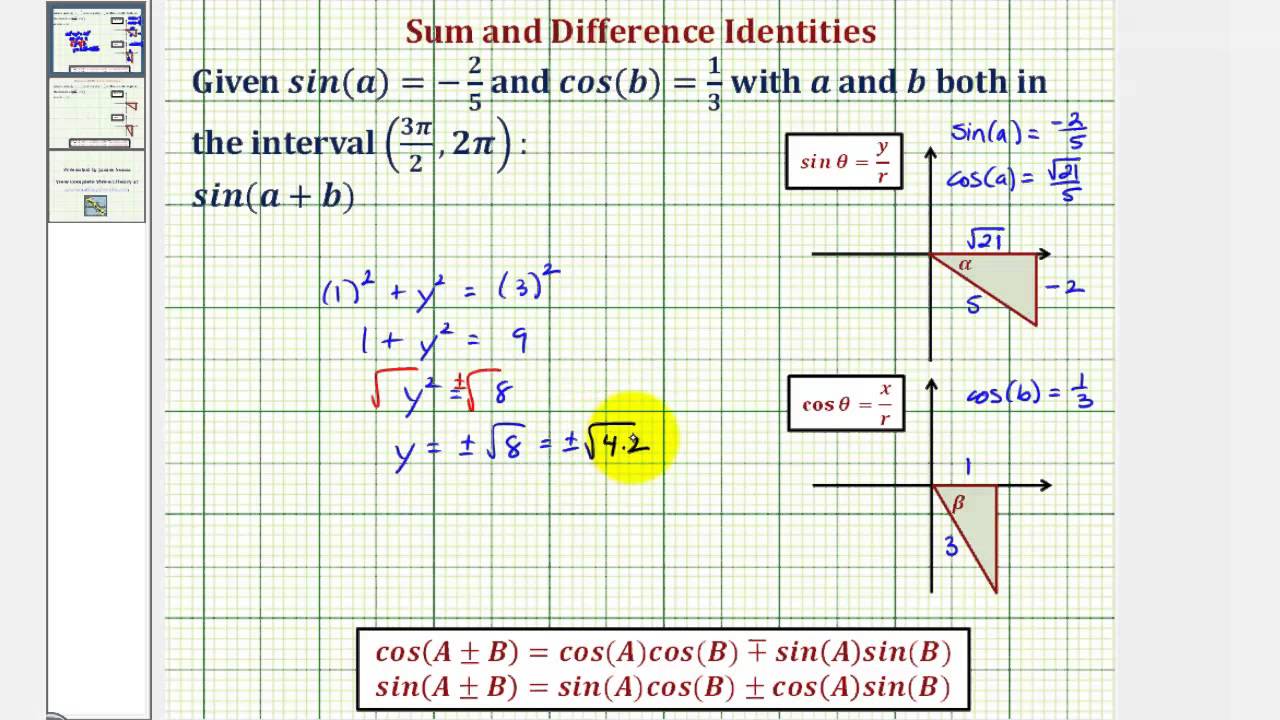



Ex Find Sin A B And Cos A B Given Sin A And Cos B Youtube
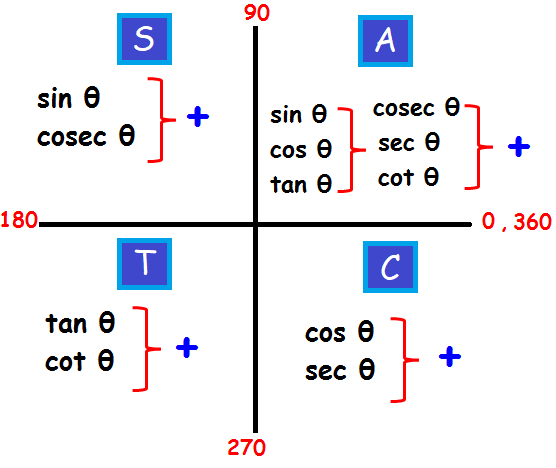
Misc 10Find sin 𝑥/2, cos 𝑥/2 and tan 𝑥/2 for sin𝑥 = 1/4 , 𝑥 in quadrant IIGiven that x is in quadrant IISo, 90° < x < 180° Replacing x with 𝑥/2(90°)/2 < 𝑥/2 < (180°)/2 45° < 𝑥/2 < 90° So, 𝑥/2 lies in Ist quadrantIn Ist quadrant, sin , cos & tan are positivesin 𝑥/2 , (टीचू) If cosx = 2/3 and x is in quadrant 4 find sin(x/2), cos(x/2), and tan(x/2) please show steps 1 See answer Advertisement Advertisement ksrcollins is waiting for your help Add your answer and earn points jdoe0001 jdoe0001 Since we have the cosine of the angle, for the halfangle identities is all we need in this case, since In Quadrant 1 , angles are from 0 to 90° In Quadrant 2 , angles are from 90 to 180° In Quadrant 3 , angles are from 180° to 270° In Quadrant 4 , angles are from 270 to 360° To learn sign of sin, cos, tan in different quadrants, we remember A dd → S ugar → T o → C offee



The Trigonometry Functions




Sine Cosine And Tangent In The Four Quadrants Teachablemath
Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high Transcribed image text 2 (2 pts) If cos (t) = 1/7 and t is in the 4th quadrant, find sin (t), tan (t), cot (t), sec (t) and esc (t) 3 (2 pts) If sin (t) = 3/4, and t is in quadrant II, find cos (t), tanAnswer to If sin theta = 4 / 5 and theta is in the first quadrant, find the values of other five trigonometric ratios By signing up, you'll getThe inverse tangent function, tan−1(a) tan − 1 ( a) is sometimes called the arctangent function, and notated arctan(a) arctan ( a) Caution47 Based only on the definitions above, the inverse trigonometric functions are not actually functions at all!



Sum And Difference Identities Precalculus Ii




Astc Formula
Answer (1 of 2) Given, tan x =3/4 and x lies in 2nd quadrant From that were are sure about the coordinate position ie (x,y)=(4,3) From pythagoras theorem, Then, cos x=b/h Cos x=4/5 We knew, cos x= 2 (cos x/2)^2 1 * 4/5 1 =2( cos x/2)^2 * 1/10 = (cosx/2)^2 Hence, Cos x /2 =/Cos x cos y sin x sin y with x y I if x is in 2nd quadrant 1 2 \u03c0 \u03c0 x \u03c0 2 y y 0 Cos x cos y sin x sin y with x y i if x is in 2nd School Eindhoven University of Technology;




Sine Cosine And Tangent In Four Quadrants
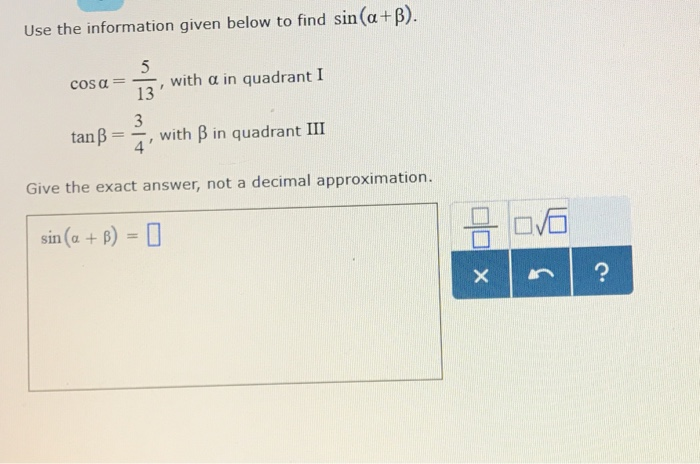



Find Sin 2x Cos 2x And Tan 2x If Cosx And X Chegg Com



Find Sin X 2 Cos X 2 And Tan X 2 If Tan X 4 3 X In Quadrant Ii Sarthaks Econnect Largest Online Education Community



If Tan 8 Is Positive And Sin 8 Is Negative In Which Quadrant Does 8 Lie Quora



Sin Cos Tan



Interborosd Org




Trigonometry Quadrant Rule Solving Sin 8 Negative Value Examsolutions Youtube



Trigonometric Ratios Solutions Examples Videos




If Cos X 2 12 13 And X Lies In Quadrant I Find The Values Of I Sin Youtube




Chapter 6 Trigonometry Section 6 4 Trigonometric Functions



Ppt Mathematics Trigonometry Reference Angles Powerpoint Presentation Id




Trigonometric Table From 0 To 360 Cos Sin Cot Tan Sec Cosec



Tangent Function Tan Graph Solved Examples Cuemath



Quadrant




The Unit Circle Reference Angles And Trigonometry Ppt Video Online Download




Tanx 4 3 X In Quadrant Ii Find The Value Of Sinx 2 Cosx 2 Tanx 2




Evaluating Trigonometric Functions Given A Point On The Terminal Side Trigonometry Youtube




Sine Cosine And Tangent In Four Quadrants




List Of Trigonometric Identities Wikipedia



Trigonometry Trigonometric Functions Functions In Quadrants Sparknotes




完了しました Quadrant 1 2 3 4 Sin Cos Tan Quadrant 1 2 3 4 Sin Cos Tan Gambarsaeawp




Trigonometry




Sine Cosine And Tangent In The Four Quadrants Teachablemath




完了しました Quadrant 1 2 3 4 Sin Cos Tan Quadrant 1 2 3 4 Sin Cos Tan Gambarsaeawp
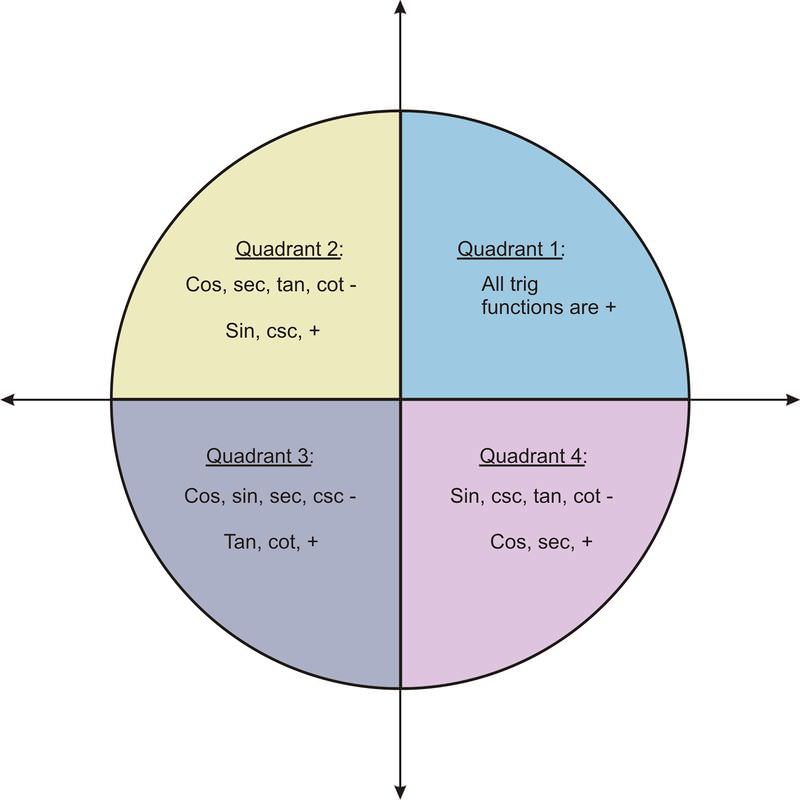



Quadrant 1 2 3 4 Sin Cos Tan



Cast Rule Mathonline
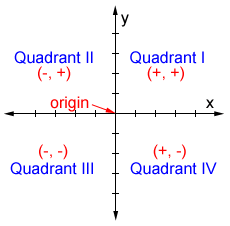



Quadrant
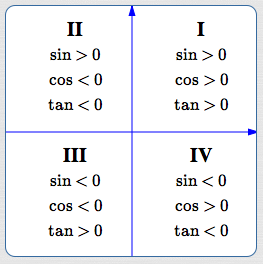



Signs Of All The Trigonometric Functions
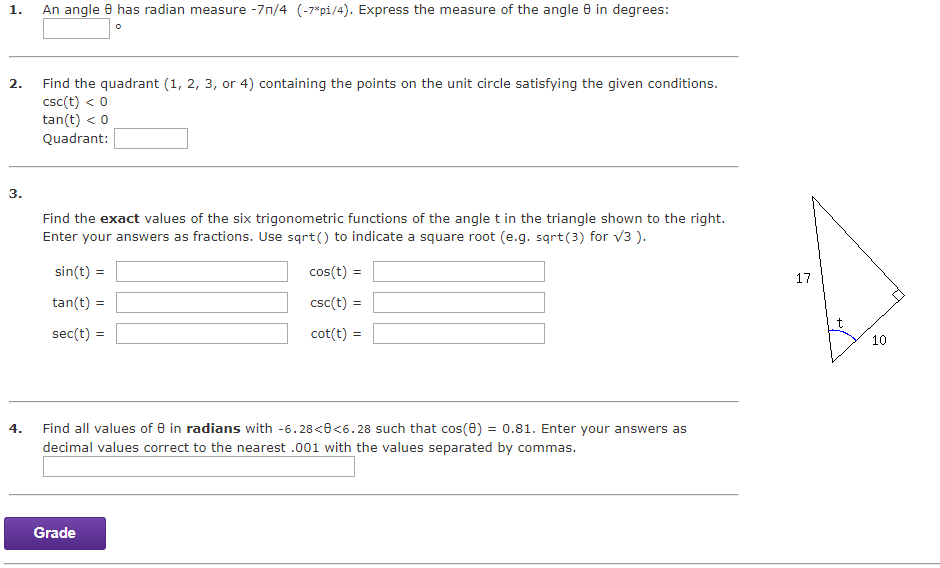



Solved 1 An Angle Has Radian Measure 7n 4 7 Pi 4 Chegg Com




Easy Way Of Memorizing Values Of Sine Cosine And Tangent Mathematics Stack Exchange




5 3 Trigonometric Ratios For Angles Greater Than 90o Ppt Download



Section 4 4 Reference Angles Precalculus




Sin Cos Tan Values Formulas Table Examples




Chapter 6 Trigonometry Ppt Download




Ex 3 2 3 If Cot X 3 5 Find Values Of Other Trigonometric




5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download




Trig Packet1 000



Sin Cos Tan



Trigonometry Sign For Sin Cos And Tan Quadrant



If P 1 1 Q 3 4 R 1 1 S 2 3 And T 4 4 Are Plotted On The Graph Paper Then The Point S In The Fourth Quadrant Is Are



Trigonometry Quadrant Formulas



What Is All Students Take Calculus In Trig Studypug




Domain And Range Of Trigonometric Functions Videos Solved Examples




Explaining Why In Different Quadrant The Angle Sine Cosine And Tangent Are Positive Or Negative Youtube




Signs Of Sin Cos Tan In Different Quadrants Finding Value Of Trign



What Trig Functions Are Positive In Which Quadrants Socratic




Trigonometric Ratios Iitutor
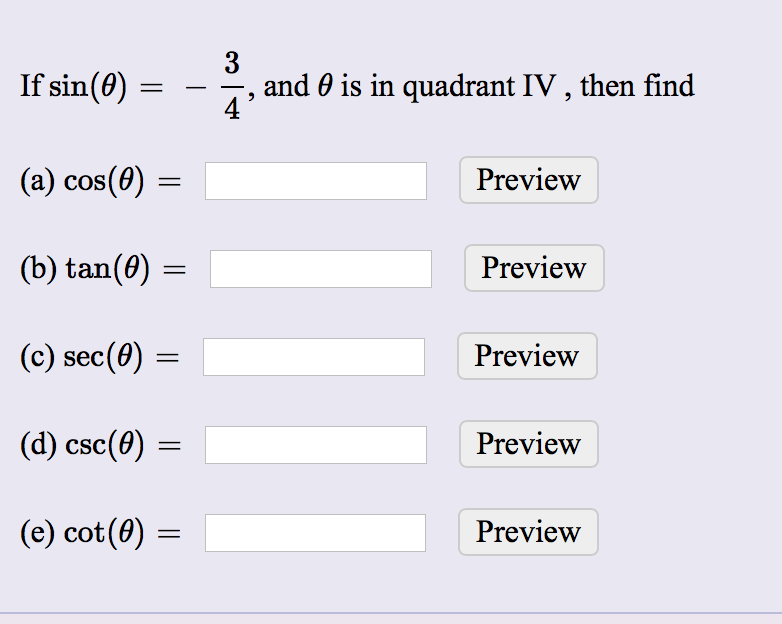



Solved If Sin Theta 3 4 And Theta Is In Quadrant Iv Chegg Com



Content The Four Quadrants
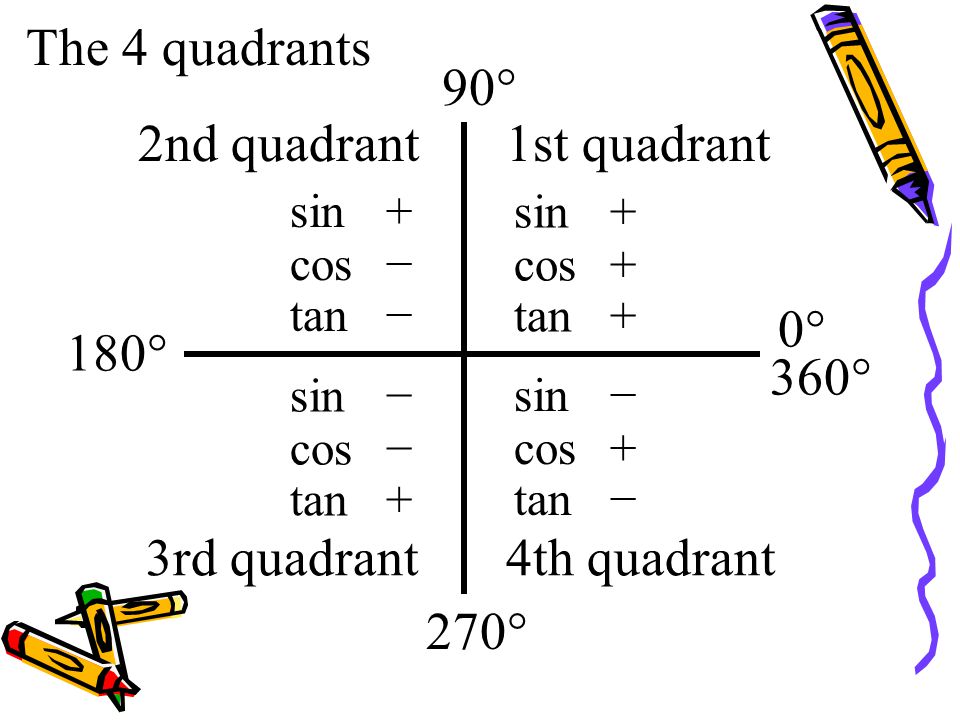



The 4 Quadrants 90 2nd Quadrant 1st Quadrant 0 180 360 Ppt Video Online Download



If Cos X 4 5 Can You Find The Value Of Sin X Quora




完了しました Quadrant 1 2 3 4 Sin Cos Tan Quadrant 1 2 3 4 Sin Cos Tan Gambarsaeawp




Sine Cosine And Tangent In Four Quadrants
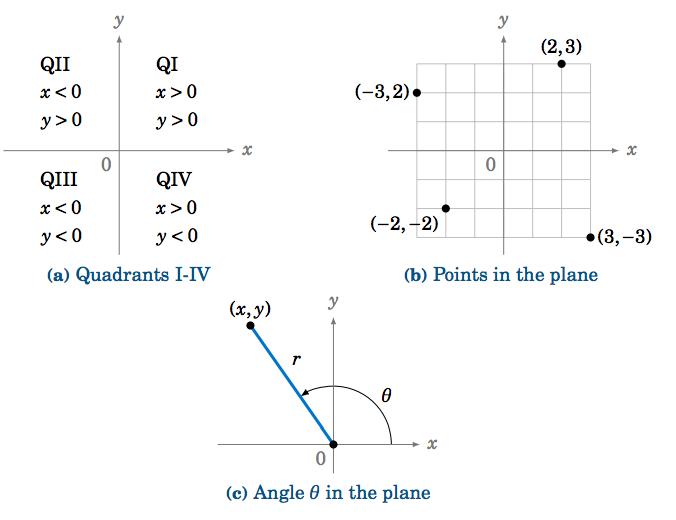



1 4 Trigonometric Functions Of Any Angle Mathematics Libretexts




All Sin Cos Tan Rule In Trigonometry Astc Rule In Trigonometry
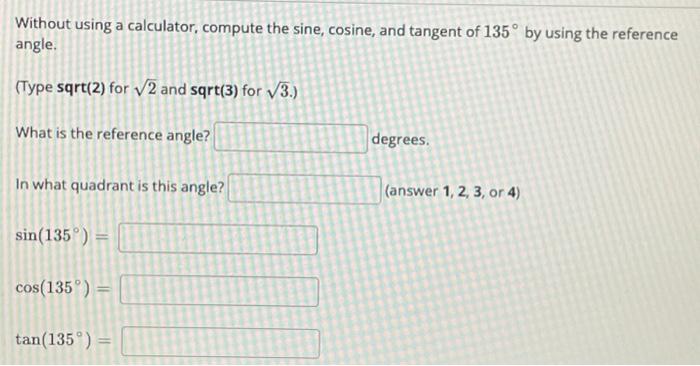



Without Using A Calculator Compute The Sine Cosine Chegg Com
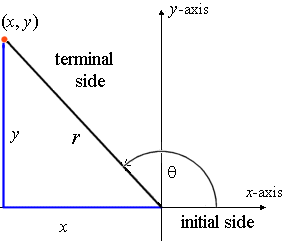



5 Signs Of The Trigonometric Functions
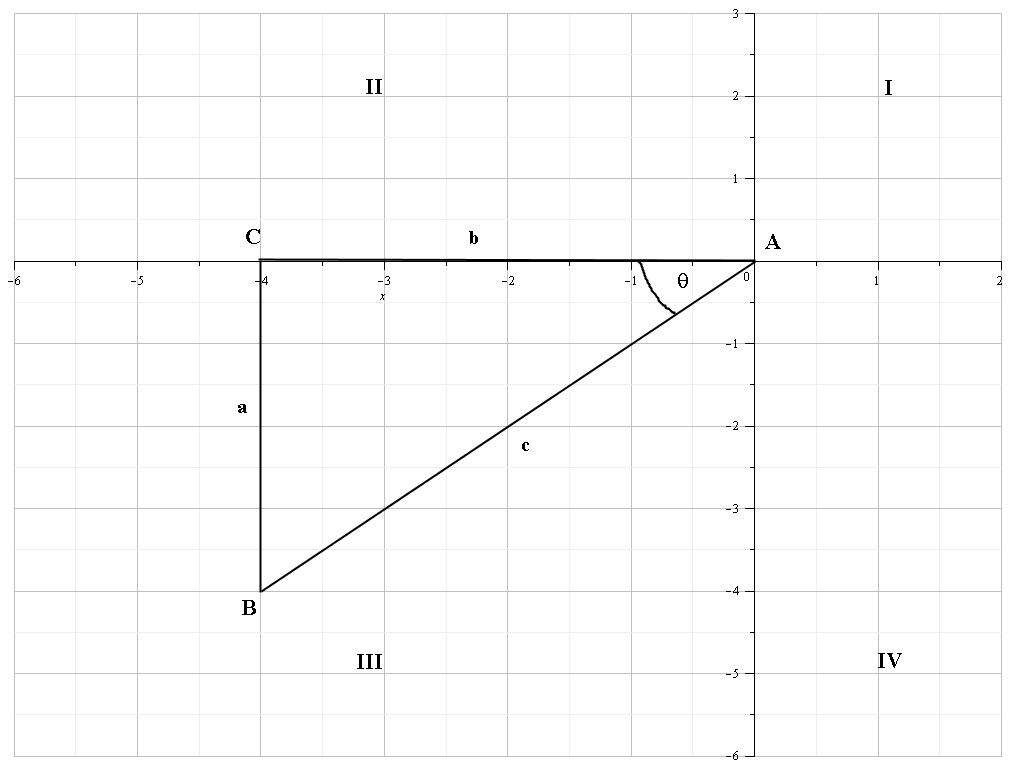



How Do You Find Sin Cos Tan Sec Csc And Cot Given 4 4 Socratic
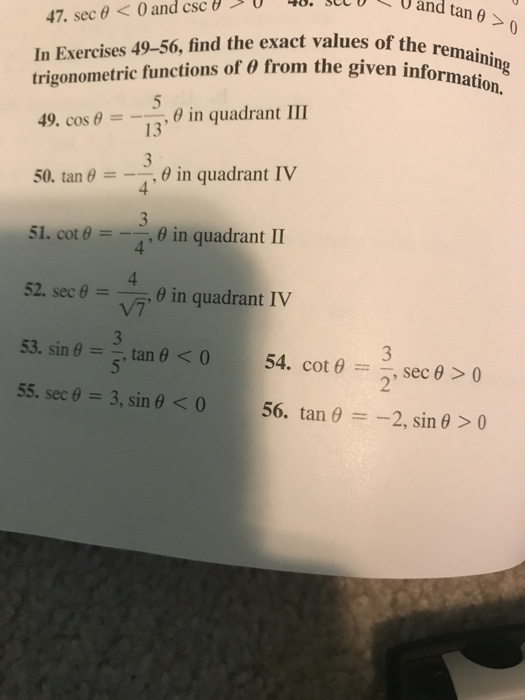



Solved Find The Exact Values Of The Remaining Trigonometric Chegg Com



Content The Four Quadrants




Quadrant 1 2 3 4 Sin Cos Tan




Page Sin 0 9511 Cos 0 3090 Tan Quadrant Iii 17 Ppt Download



Sin Cos And Tan Mathematics A Level Revision



The Trigonometry Functions




Sine Cosine And Tangent In The Four Quadrants Teachablemath



Relating Trigonometric Functions Trigonometry Socratic



If Cos 0 And Sin 0 What Quadrant Is It In Socratic



Trigonometry



If Sin Of Theta Equals 3 8 And Theta Is In Quadrant Ii What Are Cos Tan Csc Cot And Sec Of Theta Socratic



Content The Four Quadrants




If Tan Theta 3 4 And Theta Is Not In First Quadrant Then Sin Pi 2 Theta Cot Pi Theta Youtube




Cosx 1 3 X In Quadrant Iii Find The Value Of Sinx 2 Cosx 2 Tanx 2



Signs Of Sin Cos Tan In Different Quadrants Finding Value Of Trign



If Cos Theta 5 13 Theta In Quadrant Ii How Do You Find Sin Theta And Tan Theta Socratic



0 件のコメント:
コメントを投稿